The Sharpe Ratio
The previous page showed that the efficient frontier is where the most risk-efficient portfolios are, for a given collection of securities.
The Sharpe Ratio goes further: it actually helps you find the best possible proportion of these securities to use, in a portfolio that can also contain cash.
The definition of the Sharpe Ratio is:
- S(x) = ( rx - Rf ) / StdDev(x)
where
- x is some investment
- rx is the average annual rate of return of x
- Rf is the best available rate of return of a "risk-free" security (i.e. cash)
- StdDev(x) is the standard deviation of rx
The Sharpe Ratio is a direct measure of reward-to-risk.
To see how it helps you in creating a portfolio, consider the diagram of the efficient frontier again, this time with cash drawn in.
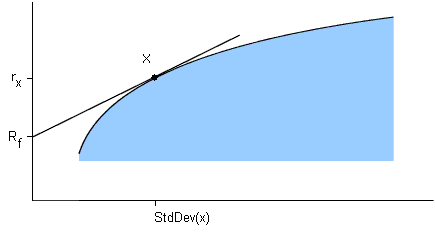
There are three important things to notice in this diagram:
- If you take some investment like "x" and combine it with cash, the resulting portfolio will lie somewhere along the straight line joining cash with x.
(This time it's a straight line, not a curve; cash is riskless, so there's no "damping out" effect between cash and x.)
- Since you want the rate of return to be as great as possible, you want to select the x that gives you the line with the greatest possible slope (like we have done in the diagram).
- The slope of this line is equal to the Sharpe Ratio of x.
Putting this all together gives you the method for finding the best possible portfolio from this collection of securities:
First, find the investment with the highest possible Sharpe Ratio (this part requires a computer);
Next, take whatever linear combination of this investment and cash will give you your desired value for standard deviation.
The result will be the portfolio with the greatest possible rate of return.
Next:
really use the Sharpe Ratio to build a risk-efficient portfolio.
|