Index Funds and Optimal Portfolios
The portfolio demo was easy to use because it assumes that the investment universe consists only of two market securities, plus riskless cash.
But of course the real investment universe is a lot bigger than that, with thousands of choices among U.S. stocks alone.
In theory you could find the optimal point on the efficient frontier generated by this many securities, but doing that wouldn't be practical.
For one thing, you'd have to calculate the covariance between every pair of securities: thousands of securities means millions of covariance calculations.
But even if you could do all those calculations, you wouldn't really want to.
That's because the efficient frontier is based on an idealized model of the way investments work; and when you apply a huge number of calculations to a model you tend to amplify the error between the model and reality, leaving you with more "noise" than anything else.
So as a practical matter, putting portfolio theory to work means reducing the problem to something about as simple as the portfolio demo, and investing in a small number of index funds rather than a huge number of individual stocks and bonds.
Index investing is where portfolio theory starts to rely on the efficient market hypothesis.
When you buy an index you're allocating your money the same way the whole market is - which is a good thing if you believe the market has a plan.
This is why portfolio theory really is a branch of economics rather than finance: instead of studying financial statements you study the aggregate behavior of investors, some of whom presumably have studied financial statements so that market valuations will reflect their due diligence.
(This viewpoint also gives rise to some bad blood that's pretty entertaining if you aren't involved.
The economists see business analysts as necessary to market efficiency, but otherwise rather beneath them as a life form, like the bacteria that make yogurt: they're useful, but they're basically germs.
The "germs" respond that the economists are delusional eggheads whose theories collapse whenever real money is involved.)
Tobin Separation Theorem
The pioneering result that helped popularize index investing was Tobin's "separation theorem", which Bill Sharpe summarized this way in an interview:
James Tobin ... in a 1958 paper said if you hold risky securities and are able to borrow - buying stocks on margin - or lend - buying risk-free assets - and you do so at the same rate, then the efficient frontier is a single portfolio of risky securities plus borrowing and lending....
Tobin's Separation Theorem says you can separate the problem into first finding that optimal combination of risky securities and then deciding whether to lend or borrow, depending on your attitude toward risk. It then showed that if there's only one portfolio plus borrowing and lending, it's got to be the market.
The reasoning behind this is easy to understand from the same kind of diagram we have already been looking at:
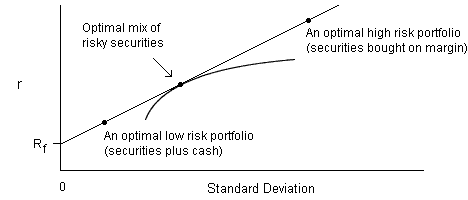
As usual you're trying to build an optimal portfolio for your risk tolerance;
and as before, it will lie somewhere on the straight line joining the cash rate Rf to some optimal mix on the efficient frontier.
We're specifically assuming what Sharpe said, that high risk investors can and will buy on margin, with money borrowed at the low rate Rf.
That's why there is just one straight line in the picture, and one unique optimal mix on the efficient frontier;
so the problem of building an optimal portfolio is "separated" into somehow finding the optimal mix and then combining it with cash to give you your desired risk tolerance.
Now for the part that's really interesting.
Assume that everybody is facing the same efficient frontier that you are, and that the market is efficient in the specific sense that it behaves in the aggregate as if everybody is trying to build an efficient portfolio this way.
That means it behaves as if everybody is on your straight line, with the same optimal mix as you.
So the mix that the market is holding - the index - is guaranteed to be your own personal optimal mix.
That's an incredibly elegant result... but it requires you to accept some really strong hypotheses.
(Two quick jabs: real investors can't afford to be so cavalier about the special risks of margin buying; and different tax brackets mean different people face different efficient frontiers.
Goodbye single straight line; so long universal optimal mix.)
Probably due to problems like those, results about index investing have trended away from proofs that index funds are optimal toward statistical models confirming that index funds are hard to beat.
That's a trend we'll be following on the next three pages, with CAPM (a theoretical model that looks like a statistical model) and the three factor model (a pure statistical model with a little theory suggested as an afterthought).
Next:
how CAPM relates individual securities to the index.
|