Capital Asset Pricing Model
Bill Sharpe made his first big breakthrough by taking the picture on the previous page and showing how the market must price individual securities in relation to their asset class (a.k.a. the index, or the "optimal mix" in the picture).
The derivation isn't exactly a walk in the park (yikes!),
but the result is a simple linear relationship known as the Capital Asset Pricing Model:
r = Rf + beta x ( Km - Rf )
where
r is the expected return rate on a security;
Rf is the rate of a "risk-free" investment, i.e. cash;
Km is the return rate of the appropriate asset class.
Beta measures the volatility of the security, relative to the asset class.
The equation is saying that investors require higher levels of expected returns to compensate them for higher expected risk.
You can think of the formula as predicting a security's behavior as a function of beta: CAPM says that if you know a security's beta then you know the value of r that investors expect it to have.
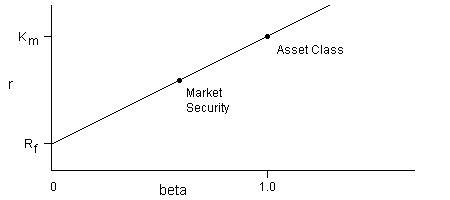
Naturally, somebody has to verify that this simple relationship actually holds true in the market.
Part of the question is how few classes you can get away with: whether you can use a very coarse division into just "stocks" and "bonds", or whether you need to divide much further (into "domestic mid-cap value stocks", and so on).
There are also ongoing attempts at "building better betas" that incorporate company debt and other traditional valuation measures, instead of relying solely on past volatility, to measure risk.
All of this is a full-time job for academic modern portfolio theorists
(and deriding the whole effort is a popular hobby for some traditional stock analysts: how could a magnificent company equal a mediocre one times beta? To them, CAPM seems like a very blunt instrument.)
CAPM has a lot of important consequences.
For one thing it turns finding the efficient frontier into a doable task,
because you only have to calculate the covariances of every pair of classes, instead of every pair of everything.
Another consequence is that CAPM implies that investing in individual stocks is pointless, because you can duplicate the reward and risk characteristics of any security just by using the right mix of cash with the appropriate asset class.
This is why followers of MPT avoid stocks, and instead build portfolios out of low cost index funds.
(One point about that last paragraph.
If you are trying to duplicate an expected return that's greater than that of the asset class, you have to hold "negative" cash, meaning you have to buy the index on margin.
This is consistent with the big message of MPT - that trying to beat the index is inherently risky).
Next:
finding CAPM from linear regression.
|