Annuity
Among other reasons, annuitized payouts are important because they're the key to retirement accounts.
You start with a lump sum at the start of retirement, and assume it's invested at a set rate of return.
Then you start to draw money out annually, for income.
The problem is to find how much these annual withdrawals can be without depleting the account too early.
To keep things simple, we'll assume that the withdrawals are all equal.
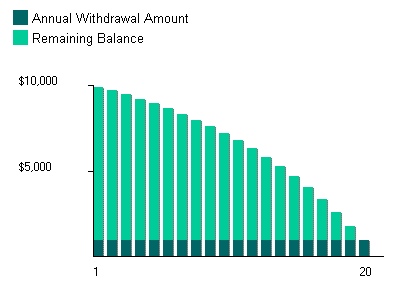
First of all, let's take a moment to appreciate that this is not a simple problem, because it incorporates two conflicting trends:
you have compound interest building the account up; at the same time you've got the investor greedily trying to suck it dry.
We'll write w for the annual withdrawal amount, and again write z for (1 + r) to keep things neater.
Writing out the first few terms for the balance,
| Year | Balance |
| 1 | P - w |
| 2 | (P - w)z - w |
| 3 | [(P - w)z - w]z - w |
Multiplying the right sides out yields the pattern:
| Year | Balance |
| 1 | P - w |
| 2 | Pz - w(1 + z) |
| 3 | Pz2 - w(1 + z + z2) |
| Y | PzY-1 - w(1 + z + z2 + . . . + zY-1) |
The second part of the last line is w times the sum of a geometric series.
So the formula simplifies to:
| 1. |
Balance(Y) = PzY-1 - w[(zY - 1)/(z - 1)]
|
We're assuming that P, r, and Y are all known and that we want to find w that makes the balance go to zero at time Y; so set Balance(Y) = 0 and solve for w, to get:
| |
0 = PzY-1 - w[(zY - 1)/(z - 1)]
|
| |
w = [PzY-1]/[(zY - 1)/(z - 1)]
|
| 2. |
w = [PzY-1(z - 1)]/[zY - 1]
|
Finally, write z out in terms of r, to get the annuity formula:
| 3. |
w = [ P(1 + r)Y-1r ] / [ (1 + r)Y - 1 ]
|
Timing Issues
The formula above assumes payouts occur at the start of each year (the idea being that that's the most natural assumption for a retirement account - you need to withdraw money now to live on for the rest of the year).
Technically that's an annuity due - an ordinary or immediate annuity assumes you get payouts at the end, which essentially means you get one more period of compounding before each payout:
| Year | Balance |
| 1 | Pz - w |
| 2 | Pz2 - w(1 + z) |
| 3 | Pz3 - w(1 + z + z2) |
| Y | PzY - w(1 + z + z2 + . . . + zY-1) |
Solving for w thus gives you one more year of growth:
| 3a. |
w = [ P(1 + r)Yr ] / [ (1 + r)Y - 1 ]
|
(The annuity calculator will let you see how much of a difference this makes.)
Present Value of an Annuity
If you solve either equation 3 or 3a for P, you get the formula for the present value of an annuity, i.e. the starting principal you'll need to achieve the payouts desired:
| 4. (annuity due) |
P = w [ (1 + r)Y - 1 ] / [ (1 + r)Y-1r ]
|
| 4a. (ordinary annuity) |
P = w [ (1 + r)Y - 1 ] / [ (1 + r)Yr ]
|
home |
article |
glossary |
calculator |
about us |
books
| 
