Mortgage
You can think of a mortgage as either building up equity or paying off debt.
Although the payments are all equal, equity doesn't build up at a constant rate:
that's because at the beginning the debt is still high, so most of the payments are paying interest;
toward the end, the remaining debt is small so very little of the payment goes toward interest.
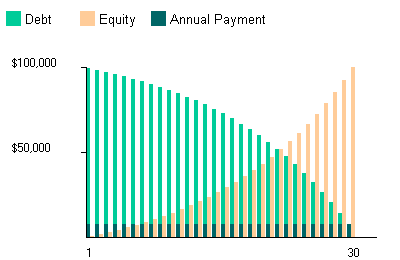
Note that for convenience we're showing the payments as annual rather than monthly.
Obviously nobody really does it that way, so if you want the correct number for a monthly payment on a mortgage use the
calculator (or see the example below).
Also, to make the graph look nicer we're showing debt at the beginning of each year, and equity at the end.
If you look at what's happening to the debt, you'll see it's similar to an
annuity
only now you're paying the balance off rather than using it up.
Also, the timing is slightly different: you make your first payment at the end of the first year.
We'll write "a" for the annual payment amount, and as usual write z for (1 + r);
P is the initial loan amount, and r is the loan interest rate expressed as a decimal.
Writing out the remaining debt at the end of the first few years,
| Year | Debt |
| 1 | Pz - a |
| 2 | (Pz - a)z - a |
| 3 | [(Pz - a)z - a]z - a |
Multiplying the right sides out yields the pattern:
| Year | Debt |
| 1 | Pz - a |
| 2 | Pz2 - az - a |
| 3 | Pz3 - az2 - az - a |
| Y | PzY - a(1 + z + z2 + . . . + zY-1) |
The second part of the last line is a times the sum of a geometric series.
So the formula simplifies to:
| 1. |
Debt(Y) = PzY - a[(zY - 1)/(z - 1)]
|
We're assuming that P, r, and Y are all known and that we want to find a that makes the debt balance go to zero at time Y; so set Debt(Y) = 0 and solve for a, to get:
| |
0 = PzY - a[(zY - 1)/(z - 1)]
|
| |
a = [PzY]/[(zY - 1)/(z - 1)]
|
| 2. |
a = [PzY(z - 1)]/[zY - 1]
|
Finally, write z out in terms of r, to get the mortgage formula:
| 3. |
a = [ P(1 + r)Yr ] / [ (1 + r)Y - 1 ]
|
Mortgage Example
Suppose you take out a 30 year mortgage for $100,000 at 7% interest, and want to know the monthly payments.
To do that, you divide the interest rate by 12 to get (.07/12) = .00583; and multiply 30 x 12 = 360 to get the number of payments.
Then the formula gives you:
payment = [$100,000(1 + .00583)360 x .00583] / [(1 + .00583)360 - 1]
= $665
home |
article |
glossary |
calculator |
about us |
books
| 
