Periodically and Continuously Compounded Interest
Back when Elvis was King and computers were scarce (and could that really be just a coincidence?) banks used to compound interest quarterly.
That meant that four times a year they would have an "interest day", when everybody's balance got bumped up by one fourth of the going interest rate...
and bank employees would have to work late, going home all sweaty and covered with ink.
If you held an account in those days, every year your balance would increase by a factor of (1 + r/4)4.
Today it's possible to compound interest monthly, daily, and in the limiting case, continuously, meaning that your balance grows by a small amount every instant.
To get the formula we'll start out with interest compounded n times per year:
FVn = P(1 + r/n)Yn
where P is the starting principal and FV is the future value after Y years.
To get to the continuous case we take the limit as the time slices get tiny:
FV =
|
limit P(1 + r/n)Yn
n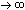
|
We can simplify the right side by introducing a new variable, defining m = n/r
FV =
|
limit P(1 + 1/m)Ymr
m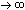
|
| |
=
|
P
|
[limit (1 + 1/m)m]Yr
m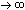
|
The limit in the square brackets converges to the number e = 2.71828....
(In fact, Leonhard Euler may have thought of this limit as the definition of e, right around the time he named it "e" after himself).
So the formula becomes
FV = PeYr
This calculator lets you see how fast the formula converges.
Incidentally, if you know calculus then the continuous compounding formula has a natural interpretation.
First let's replace the clunky "FV" notation, and write f(t) for the balance at time t (with t measured in years).
So
f(t) = Petr
Taking the derivative
|
|
f(t) =
|
|
(Petr)
|
|
=
|
rPetr
|
|
=
|
r f(t)
|
In words, this is saying that
"at any instant the balance is changing at a rate that equals r times the current balance"
which of course is the definition of continuous compounding.
home |
article |
glossary |
calculator |
about us |
books
| 
