CAGR
CAGR (for Compound Annual Growth Rate) is the hypothetical constant interest rate that would be required for
compound interest to turn a given present value into a given future value in a given amount of time.
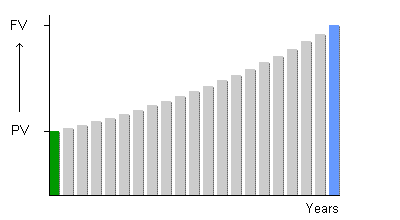
|
(In this graph, CAGR would be the interest rate required to grow the green bar into the blue bar.)
|
The CAGR formula is
CAGR = (FV / PV)1 / Y - 1
where PV and FV are the present value and future value, and Y is number of years.
See the explanation of the CAGR formula and the
CAGR calculator.
CAGR Examples and Calculations
It's easy to calculate the CAGR by the equation above, as long as you really are given only three inputs
(present value, future value, and years).
One example is the "average" inflation rate in the US, which is really the CAGR defined by applying the
formula to the appropriate values of the Consumer Price Index (CPI).
For example, the USA experienced deflation during the 1930s, with the CPI falling from 17.2 to 14.0 over the decade.
Plugging these values into the CAGR formula gives a negative annualized inflation rate:
i = (14.0 / 17.2)1 / 10 - 1 = -2.04%
When deposits or withdrawals occur during the time period, calculations are harder.
You can estimate the CAGR easily for short time periods (like one year).
The more general case requires a spreadsheet or computer program, instead of a simple formula.
You have to keep track of capital gains, deposits, and withdrawals as they occur, apply them to the FV as a running total, and finally use the equation above.
This is how to calculate stock market returns including dividends.
CAGR versus Reality
CAGR is a hypothetical constant growth rate, which means it gives you a smoothed-out version of the world with no volatility.
Ignoring volatility can be dangerous in financial planning:
see Risk and your Time Horizon.
|