Investment Valuation with DCF: A Little Theory
We'll start with a little theory before we get to the calculators.
A company is valuable to stockholders for the same reason that a bond is valuable to bondholders:
both are expected to generate cash for years into the future.
Company profits are more volatile than bond coupons, but as an investor your task is the same in both cases:
make a reasonable prediction about future earnings, and then "discount" them by calculating how much they are worth today.
(And then you don't buy unless you can get a purchase price that's less than the sum of these present values, to make sure ownership will be worth the headache.)
Let's take an example.
Suppose you are interested in a company that earned $10 per share over the last twelve months.
Assume you expect the company to grow over the foreseeable future, so that its earnings will grow at a rate of 8% annually for the next 10 years;
then, to play it safe, you make no assumptions about earnings after that, but just expect the company to stay at the same size from then on.
Your earnings expectations look like this:
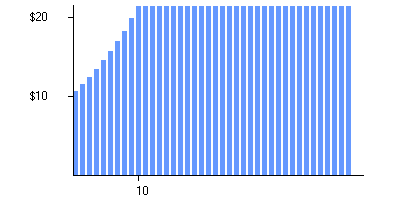
Here the height of each blue bar is the earnings per share that you expect for a particular year in the future.
(The first bar is earnings over the next twelve months: that is, it's what you expect the company's reported annual earnings to be one year from now.)
Now for the discounting, finding how much each "blue bar of the future" is worth to you in the present.
We'll be using a discount rate of 11%, which is about the average annual return rate of the stock market over the past many decades.
The idea is that earnings of $1.11 next year is only worth $1.00 to you right now, since you could invest the $1.00 in the S&P 500 and expect it to grow to $1.11 in one year's time.
Finding the present value of all of the blue bars gives a new graph:
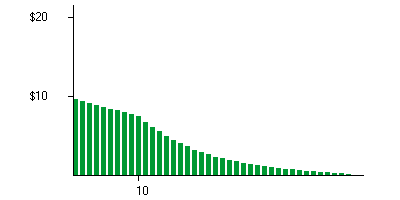
Here each green bar is the value to you, today, of each corresponding blue bar in the first graph.
If you want to check into this in a little more detail, use the popup calculator in
future value mode
to find that $10 per share growing at 8% annually will grow to $21.59 in 10 years (that's the height of the blue bar at year 10);
and then in
present value mode
to find that $21.59 10 years from now is worth $7.60 today assuming a discount rate of 11%
(that's the height of the green bar at year 10).
We've drawn both graphs with forty bars, but the valuation formulas we'll use in the calculators assume the company will keep going forever: an infinite number of bars.
But the key is that the green bars are shrinking so rapidly that, even though there are an infinite number of them, if you stacked them up they would only reach a finite height: in this example, the height would be $155.40.
That total - the sum of the present values of all future earnings - is the theoretical value of the investment right now.
(See detail.)
How Long is Forever?
The last paragraph said we'd assume earnings would be going on forever into the future - not exactly a realistic assumption.
But it turns out that assumption isn't really important: the rapid shrinkage of the green bars means that any contribution from the distant future is negligible.
In this example, all earnings after year 50 contribute only about one dollar - less than 1% - to the stock's value today:
What are "Earnings"?
Purists would say that a company is worth the present value of its future free cash flows rather than its earnings.
The trouble is that you would have to know a lot about the company (and use fancier calculators!) to find values with FCF.
So we'll assume that earnings and free cash flow are equivalent in the long run, and that both approximate real cash profits.
What about Debt?
What does debt do to the value of a company?
The quick answer is that any valuation based on earnings has already accounted for debt.
That's because interest payments - the "cost" of the debt - are an expense, and have already been deducted from earnings.
So if the present value of future earnings adds up to $20 a share, the company's stock is worth $20 a share, regardless of the amount of debt it has.
Of course the real world is more complicated than that glib theoretical answer; for example:
- Debt is better than that: interest is an expense, so debt financing gives business a tax break unavailable with other forms of financing.
- Debt is worse than that: interest is an absolute obligation, so debt increases the risk that some years will have low reported earnings (not to mention the risk of bankruptcy).
If you put those two contradictory statements together they actually form a coherent whole:
Debt is a cheap way for a company to raise capital; and the superior profits that result will be a reward for stock investors willing to accept the added risk.
More DCF Examples
If you'd like to try more examples like this one, see this
separate article
for an interactive graph.
home |
article |
glossary |
calculator |
about us |
books
|